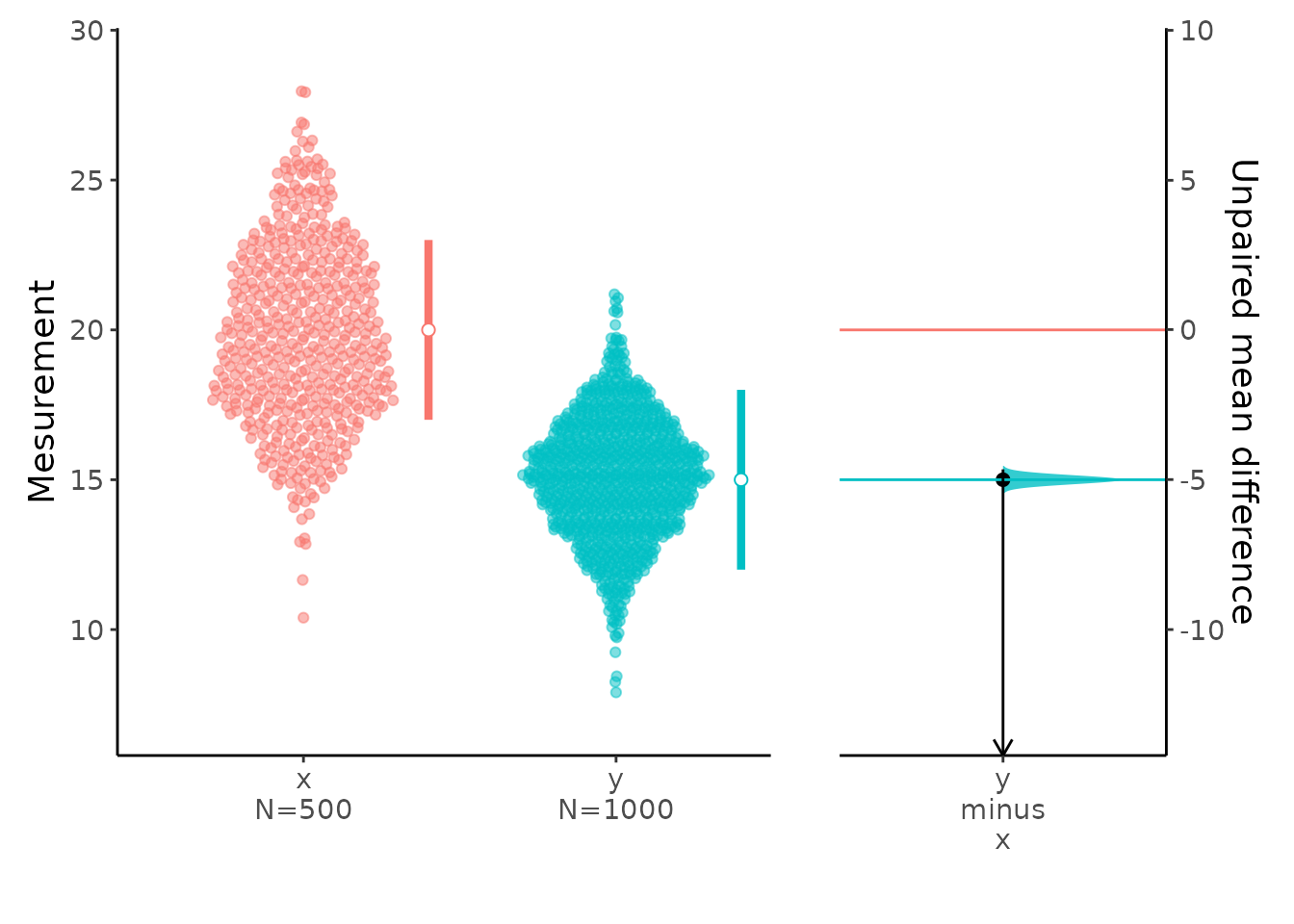
Confidence interval for the unpaired mean difference

This document is prepared automatically using the following R command.

Problem

Confidence interval of mean

The approach that we used to solve this problem is valid when the following conditions are met.

• The sampling method must be simple random sampling.

• The samples must be independent.

• The sampling distribution should be approximately normally distributed.

Since the above requirements are satisfied, we can use the following four-step approach to construct a confidence interval of mean.

Raw data

Raw data is not provided.

Identify sample statistics

Since we are trying to estimate the difference between population means, we choose the difference between sample means as the sample statistic. Thus,

\[\bar{x1}-\bar{x2}=20-15=5\]

Select a confidence level.

In this analysis, the confidence level is defined for us in the problem. We are working with a 99% confidence level.

Find the margin of error

1. Find standard error.

The standard error is an estimate of the standard deviation of the difference between population means. We use the sample standard deviations to estimate the standard error (SE).

\[SE=\sqrt{\frac{s^2_1}{n_1}+\frac{s^2_2}{n_2}}\] \[SE=\sqrt{\frac{3^2}{500}+\frac{2^2}{1000}}\] \[SE=0.148\]

2. Find the degree of freedom(df)

\[DF=\frac{(\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2})^2}{\frac{(s_1^2/n_1)^2}{n_1-1}+\frac{(s_2^2/n_2)^2}{n_2-1}}\] \[DF=\frac{(\frac{3^2}{500}+\frac{2^2}{1000})^2}{\frac{(3^2/500)^2}{500-1}+\frac{(2^2/1000)^2}{1000-1}}\]

\[DF=727.48\]

3. Find the critical value

The critical value is the t statistic having 727.48 degrees of freedom and a cumulative probability equal to 0.99. From the t Distribution table, we find that the critical value is 2.331.

\[ qt(p,df)=qt(0.99,727.48)=2.331\] The graph shows that \(\alpha\) values are the tail areas of the distribution.

4. Compute margin of error(ME)

\[ME=critical\ value \times SE\] \[ME=2.331 \times 0.148=0.346\]

5. Specify confidence interval

The range of the confidence interval is defined by the sample statistic - margin of error and the \(\infty\)(infinite). And the uncertainty is denoted by the confidence level.

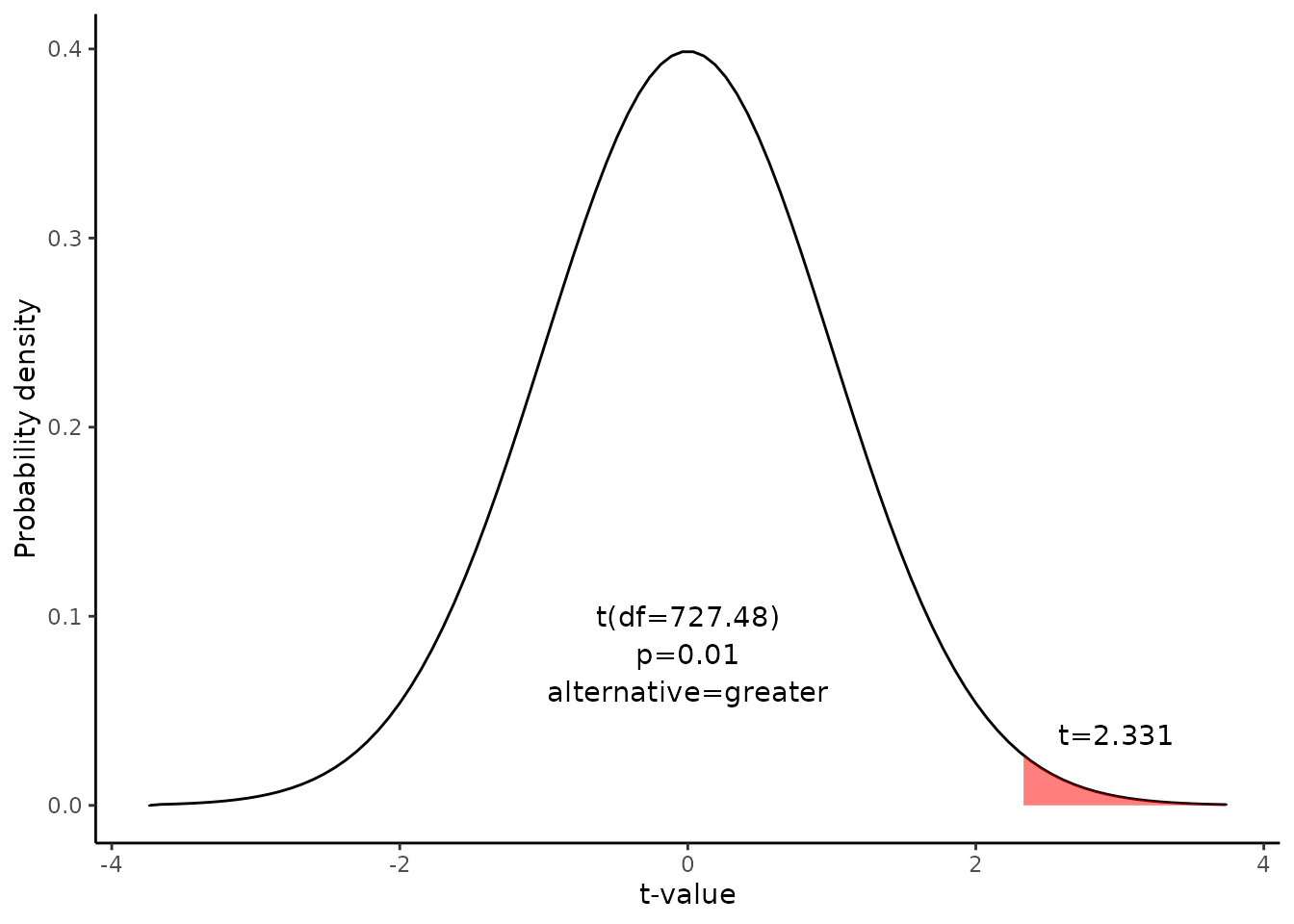
Confidence interval of the mean difference

Therefore, the 99% confidence interval is 4.65 to Inf. Here’s how to interpret this confidence interval. Suppose we repeated this study with different random samples for men and women. Based on the confidence interval, we would expect the observed difference in sample means to be between 4.65 and Inf 99% of the time.

Plot

You can visualize the mean difference:

plot(x)

Result of meanCI()

call: meanCI.default(n1 = 500, n2 = 1000, m1 = 20, s1 = 3, m2 = 15,      s2 = 2, alpha = 0.01, alternative = "greater") 
method: Welch Two Sample t-test 
alternative hypothesis:
   true unpaired differences in means is greater than  0 

Results

[38;5;246m# A tibble: 1 × 6
[39m
  control test  DF     CI                    t     p        
  
[3m
[38;5;246m<chr>
[39m
[23m   
[3m
[38;5;246m<chr>
[39m
[23m 
[3m
[38;5;246m<chr>
[39m
[23m  
[3m
[38;5;246m<chr>
[39m
[23m                 
[3m
[38;5;246m<chr>
[39m
[23m 
[3m
[38;5;246m<chr>
[39m
[23m    

[38;5;250m1
[39m x       y     727.48 5.00 [99CI 4.65; Inf] 33.71 < 2.2e-16

Reference

The contents of this document are modified from StatTrek.com. Berman H.B., “AP Statistics Tutorial”, [online] Available at: https://stattrek.com/estimation/difference-in-means.aspx?tutorial=AP URL[Accessed Data: 1/23/2022].